Régulation et boucles de Régulation
instrumentation regulation boucleGENERALITES
La conduite et le contôle de n'importe quel procédé de traitement ou production nécéssite la maîtrise des paramètres du bon fonctionnement des installations, principalement :
- la pression
- la température
- le débit
- le niveau
Nous sommes donc amenés à effectuer des "mesures" pour obtenir ces informations indispensables à assuree le bon fonctionnment des installations.
Ce contrôle sera obtenu par l'intermédiaire d'appareillages spécifiques.
Ce sont ces informations qui vont nous permettre de :
- quantifier
- comparer et vérifier,
- dupliquer, recopier, répéter
Ces informations peuvent être locales ou renvoyées en salle de contrôle.
En salle de contrôle on peut accéder à ces informations sur :
- des indicateurs
- des enregistreurs
- des écrans des consoles sur différentes vues spécifiques :
- synoptiques,
- groupes de travail
- vues de détail
- alarmes
- historiques
De façon analogue, les commandes nécessaires à la conduite du procédé s'effectuent soit sur le site, à proximité de l'appareillage, soit à partir de la salle de contrôle-commande, en manuel ou de façon automatique ou programmés sur des ordinateurs (Automates de régulation numérique).
L'objectif global de la régulation peut se résumer par ces trois mots clefs :
• mesurer ;
• comparer ;
• corriger.
Cependant, chaque procédé possède ses exigences propres, chaque appareil possède ses propres conditions de fonctionnement. Il est donc indispensable que la régulation soit conçue pour satisfaire aux besoins particuliers liés à la sécurité, aux impératifs de production et aux matériels.
La régulation est l'action de régler automatiquement une grandeur de telle sorte que celle-ci garde constamment sa valeur ou reste proche de la valeur désirée, quelles que soient les perturbations qui peuvent subvenir.
RAPPELS
GRANDEURS LOGIQUES
Les grandeurs logiques, ne peuvent prendre que deux valeurs notées 0 ou 1.
On utilise généralement une logique dite «positive »
0 : Pas d’action
1 : Action
| 0 | 1 |
|
|
GRANDEURS ANALOGIQUES
Ces grandeurs varient de façon continue (entre deux limites)
EXEMPLE : Niveau d’un réservoir

Grandeurs logiques :
Zone A : SH = 1 SL = 0
Zone B : SH = 0 SL = 0
Zone C : SH = 0 SL = 1
Les seuils haut SH et bas SL permettent de définir des niveaux logiques à Partir de la valeur analogique du niveau.
Le niveau peut varier de façon continue de 0 à 100%. C’est une grandeur analogique.
REGULATION :action de régler
La plupart des systèmes comportent une réaction naturelle qui s’oppose à l’action et conduit à un nouvel état d’équilibre.
Cet état n’est que rarement satisfaisant.
On est donc amené à concevoir des ensembles dans lesquels la grandeur désirée s’aligne rigoureusement sur une grandeur de consigne.
On y parvient en appliquant une rétroaction.
On parle de régulation quand la grandeur réglée s’aligne avec une grandeur de consigneconstante, il s’agit d’asservissement lorsque la grandeur réglée suit une grandeur de référence variable.
ELEMENTS CONSTITUTIFS D’UNE BOUCLE DE REGULATION
Une boucle de régulation doit comporter au minimum les éléments suivants :
- un capteur de mesure ;
- un transmetteur souvent intégré au capteur ;
- un régulateur ;
- un actionneur.
Elle est souvent complétée par :
- un enregistreur ;
- des convertisseurs ;
- des sécurités.
SCHEMA DE PRINCIPE D'UNE BOUCLE DE REGULATION

Le régulateur reçoit deux informations :
- Le signal de mesure (M ou PV) provenant du capteur,
- la consigne (C ou SP) (qui peut être locale ou externe)
En fonction de l'écart entre ces deux valeurs et de l'algorithme de calcul pour lequel il a été configuré, il délivre un signal de sortie (S ou OUT) dirigé vers l'actionneur afin d'annuler cet écart et de ramener la mesure vers la valeur de consigne.
Le régulateur est le "cerveau" de la boucle de régulation.
NATURE DES SIGNAUX
Les signaux reçus et transmis par le régulateur doivent être normalisés afin de permettre l'interchangeabilité du matériel.
Ils peuvent être de nature différente :
- Electriques
- Pneumatiques
- Numériques
- Plus rarement hydrauliques
Ces signaux sont normalisés
| NATURE DU SIGNAL ANALOGIQUE | VALEURS NORMALISEES LES PLUS COURANTES |
| non définis | |
| électriques | 4<i<20 mA |
| pneumatiques | 200<P<1000mb |
| numériques | codées sur 8, 16, 32, ... bits |
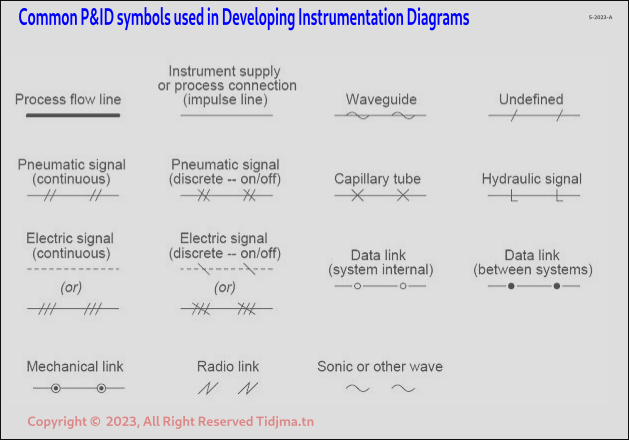
En électrique (intensité) :
- 0% échelle ----> 4 mA
- 100% échelle ----> 20mA
En pneumatique (pression) :
- 0% échelle ----> 200 mb (3 psi)
- 100% échelle ----> 1000mb (15 psi)
En numérique, les signaux sont codés en binaire sur 8, 16, 32 ou 64 bits en liaison série ou parallèle.

En fonction de la nature des capteurs, des actionneurs et des régulateurs (analogiques ou numériques) des convertisseurs sont indispensables à différents points de la boucle pour normaliser les signaux.
EXEMPLE
Capteur de niveau par sonde hydrostatique
Régulateur numérique (ordinateur)
vanne automatique à ouverture analogique à commande pneumatique
SCHEMA DE PRINCIPE D’UNE BOUCLE DE REGULATION COMPLEXE

- jauge hydrostatique
- convertisseur Pression / Intensité
- convertisseur Analogique / Numérique
- convertisseur Numérique / Analogique
- convertisseur Intensité / Pression
- vanne automatique à commande pneumatique
LES CAPTEURS DE MESURE
Un capteur est l'élément d'un appareil de mesure servant à la prise d'informations relatives à la grandeur à mesurer.
Le capteur est l'élément capital et le premier maillon d'une chaîne de mesure.
Il a pour rôle de saisir et de transformer la grandeur physique à mesurer (ou mesurande) et le contenu de son information en une autre grandeur physique accessible aux sens humains ou aux maillons suivants de la chaîne d'acquisition.
Ce sont donc des organes sensibles, transformant la grandeur à mesurer en un signal électrique, pneumatique, hydraulique ou numérique, normalisé, représentatif de l'information originelle.
Cette transformation nécessite généralement un apport d'énergie extérieure au système.
En règle générale, l'élément sensible du capteur est lié à un traducteur ou transducteur permettant la transformation du déplacement ou de la déformation de cet élément sensible en un signal ou une indication de mesure.
SCHEMA DE PRINCIPE

Par simplification, l'ensemble est appelé CAPTEUR.
PRINCIPES DE QUELQUES CAPTEURS
MESURES ET CAPTEURS DE PRESSION
DEFINITION : Une force pressante F s'exerçant uniformément sur toutes les parties d'une surface S
détermine une pression P telle que P = F/S
REMARQUE : Une pression dans un fluide peut s'exprimer en hauteur de colonne de fluide. Une mesure de pression peut donc permettre la détermination d'un niveau dans un récipient.11
DESIGNATION DES PRESSIONS :

1, 2 : pressions relatives (ou effectives)
3, 4 : pressions absolues
5, 6 : pressions différentielles
PRESSIONS DANS UN FLUIDE EN MOUVEMENT
- Ps : Pression statique
- Pd : Pression dynamique
- Pt : Pression totale

MESURES ET CAPTEURS DE NIVEAU
De très nombreux systèmes sont utilisés. Ilimportant de connaître un certain nombre de paramètres indispensables pour choisir le capteur le mieux adapté qui sont notamment :
- la nature du fluide
- les propriétés physiques et chimiques du fluide
- la précision recherchée dans la mesure
- les indication directe ou à distance
- les conditions de sécurité
MESURES ET CAPTEURS DE DEBITS
Plusieurs techniques peuvent être mises en œuvre. L'intégration dans le temps du débit permet d'accéder au comptage.
On trouve essentiellement :
- des compteurs volumétriques
- des turbines
- des débitmètres électromagnétiques, à effet Vortex, à ultrasons, massiques, à cible
- des tubes de Pitot et de Prantl
- des organes déprimogénes : diaphragme, venturi, tuyère.
CONTROLE DES TEMPERATURES
Les thermomètres à dilatation ou à changement d'état sont généralement utilisés en local.
Les deux dispositifs les plus utilisés actuellement pour la télémesure sont :
Les thermocouples
Pour qu’il y ait «couple » c’est à dire pour qu’il se produise un effet thermoélectrique, il
faut que deux conducteurs de nature différente, en liaison électrique, soient soumis à des températures différentes.
Les sondes à résistance de platine (Pt100) ou à thermistances
Tous les conducteurs métalliques voient leur résistivité varier en fonction de la température. Pour les métaux, la résistivité augmente avec la température. Le platine est pratiquement le seul conducteur utilisé.
En règle générale on utilise des sondes de 100 ohm à 0°C (Pt 100)
Les pyromètres optiques sont généralement utilisés dans le domaine des hautes températures.
ETALONNAGE D’UN CAPTEUR DE NIVEAU
Le capteur de niveau donné en exemple est du type piézorésistif.
Sa résistance est fonction de la pression qu’il subit.
La pression étant liée à la hauteur de fluide par la relation P = ρgh, il peut être utilisé pour une mesure de niveau.
Données constructeur :
0 cm CE 4 mA
200cm CE 20 mA
MODE OPERATOIRE
On dispose d’un réservoir gradué d’environ 60cm de hauteur, d’un mA et d’un régulateur analogique utilisé en afficheur.
On démarre réservoir vide, puis on augmente progressivement la hauteur d’eau dans le réservoir en notant à intervalles réguliers après 10 secondes de stabilisation, la hauteur d’eau dans le réservoir, l’intensité dans la boucle de mesure et l’indication affichée sur le régulateur.
A la dernière mesure, on note l’évolution de l’intensité dans la boucle de mesure en fonction du temps, le niveau dans le réservoir restant stable afin de vérifier la stabilité de la réponse.
SCHEMA DE MONTAGE
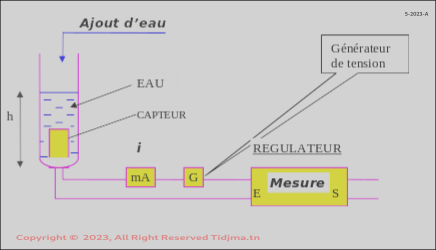
TABLEAU DE MESURES
I et M en fonction de H

REPRESENTATIONS GRAPHIQUES
Im =f (h)
La hauteur du réservoir étant inférieure au maximum de l’échelle, il est
indispensable d’extrapoler la courbe jusqu’à une intensité de 20mA afin de déterminer le point 100% d’échelle.
Cette courbe nous permet de déterminer le 0 et le 100% d’échelle, d’où l’étendue d’échelle, la linéarité (dans la zone testée expérimentalement), un éventuel décalage et l’équation de la courbe.
M = f (h)
Cette courbe permet de mettre essentiellement en évidence un décalage

entre l’échelle graduée et l’affichage de la mesure sur le régulateur.
CONVERTISSEUR ELECTROPNEUMATIQUE
Les convertisseurs P/I sont utilisés pour convertir en standard électronique les signaux pneumatiques dans le but de les transmettre sur une grande distance ou de les utiliser en régulation électronique.
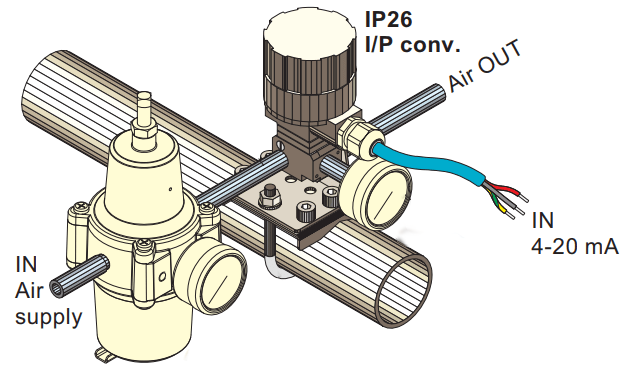
Les convertisseurs I/P sont utilisés dans toutes les boucles électroniques dont l’actionneur est pneumatique ou par exemple pour la traversée de zones explosives. Ils transforment les signaux électriques normalisés en signaux pneumatiques normalisés.
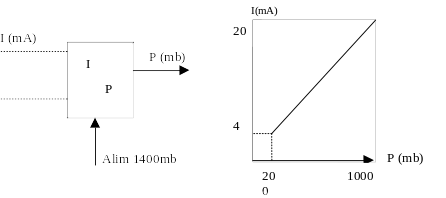
Dans le cas d’un convertisseur électro-pneumatique, celui-ci reçoit un signal 4-20mA et renvoie une pression de 200 à 1000 mb.
Le convertisseur est alimenté par une pression d’air de 1400 mb.
ETALONNAGE DU CONVERTISSEUR
SCHEMA DE MONTAGE
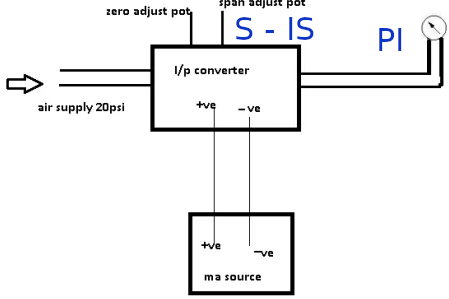
MODE OPERATOIRE
Le régulateur étant placé en mode MANUEL, on fait varier le % de sortie S et on note S%, l’intensité de sortie IS du régulateur (entrée convertisseur) et la pression PI de sortie du convertisseur.
LES ORGANES DE COMMANDE (ACTIONNEURS OU EFFECTEURS)
Tout comme les informations, les commandes peuvent être de nature différente :
- logiques : mise en marche/arrêt des pompes, interrupteurs, moteurs,...
- analogiques : ouverture plus ou moins grande de vanne de réglage, puissance de chauffe,...
Lorsque la commande est directement asservie à l'indication d'un capteur et ne nécessite pas l'intervention directe de l'homme, on peut, selon le cas parler d'automatisme ou de boucle de régulation.
VANNES AUTOMATIQUES DE REGULATION
La plupart des réglages se ramènent à des réglages de débits de fluides au moyen d'appareils de robinetterie créant une perte de charge sur la circulation du produit.
Les vannes sont des organes comportant un orifice de dimension variable. Elles permettent le réglage des débits de fluides.
Le débit est proportionnel à la racine carrée de la perte de charge entre l’amont et l’aval de la vanne.
CARACTERISTIQUES DE DEBIT
On appelle caractéristique d'une vanne régulatrice la relation qui lie la levée du clapet au débit qui traverse cette vanne à perte de charge constante. On rencontre trois types de caractéristiques liées à la géométrie des clapets.
- caractéristique exponentielle ou égal %
- caractéristique linéaire
- caractéristique "ouverture rapide"
Les vannes de régulation les plus employées sont équipées de clapet double siège.
Ces vannes ne sont jamais parfaitement étanches. Sur les circuits qui nécessitent un sectionnement étanche, on est amené à installer des vannes étanches à fonctionnement "tout ou rien".
La plupart des constructeurs indiquent le débit de la vanne en gallons US par minute lorsque la perte de charge créée par la vanne est de 1 PSI (vanne grande ouverte S = 100%).
C’est le coefficient de débit de la vanne Cv.
Le Kv de la vanne est son débit d’eau en m3/s pour une perte de charge de 1 bar, vanne grande ouverte
Cv = 1.16 Kv17
ETALONNAGE DE L’ACTIONNEUR
SCHEMA DE MONTAGE
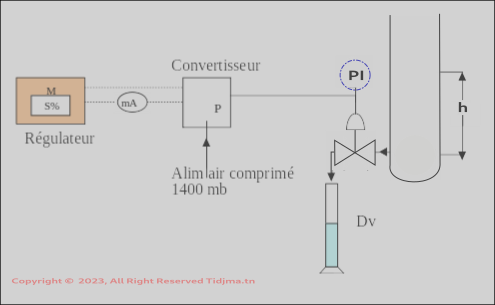
MODE OPERATOIRE
Caractéristique de la vanne :
On fixe la hauteur (h) d’eau dans le réservoir à une hauteur arbitraire que l’on maintiendra constante pendant toute la manipulation (en rajoutant de l’eau dans le réservoir).
Pour différentes valeurs du signal de sortie, donc de la pression de commande de la vanne en
sortie du convertisseur, on note le débit de la vanne.
Ce débit peut être obtenu par exemple en notant le temps nessecaire pour remplir une éprouvette graduée de 100mL.
Dv = f (PI) ou Dv = f (S%)
Dv (L/h)
Cette courbe permet de définir le type de la caractéristique de la vanne

.
Débit en fonction de la perte de charge crée par la vanne
Cette manipulation permet de déterminer le coefficient de débit (CV) de la vanne
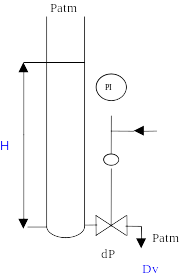
La vanne est maintenue ouverte à 100%
On fait varier la perte de charge au passage de la vanne en
modifiant la hauteur de liquide dans le réservoir
La perte de charge est égale dans ce cas à la pression
exercée par la colonne de liquide
CV =débit en Gallons US/min pour une perte de charge de
vanne ouverte à 100%
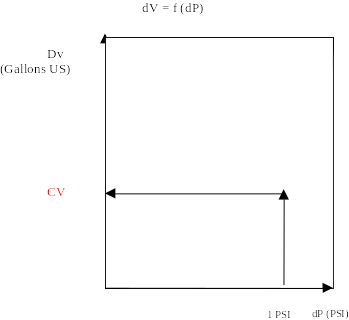
La hauteur du réservoir étant trop faible
Pour créer une perte de charge de 1 PSI,
Il est necessaire d’extrapoler la courbe
1 Gallon US = 3,785 L
1PSI = 0,069 bar
1 PSI
dP (PSI)20
ANALYSE DES PROCEDES INDUSTRIELS
Analyser un procédé industriel, c'est connaître sa réaction naturelle face à une perturbation .
Le procédé étant inclus dans une boucle ou une chaîne de régulation, la connaissance de son comportement permet de définir le correcteur associé à ce procédé, le but étant d'assurer la stabilité de l'ensemble.
Il existe de nombreuses méthodes d'analyse des procédés, certaines faisant appel à des
notions mathématiques et technologiques complexes.
CLASSIFICATION DES PROCEDES
La réaction naturelle des procédés permet de les classer en deux catégories fondamentales :
PROCEDES STABLES (autorégulants, statiques)
PROCEDES INSTABLES (intégrateurs, astatiques)
EXEMPLE DE PROCEDE STABLE

A une excitation d'entrée limitée, correspond une variation de sortie limitée.
EXEMPLE DE PROCEDE INSTABLE
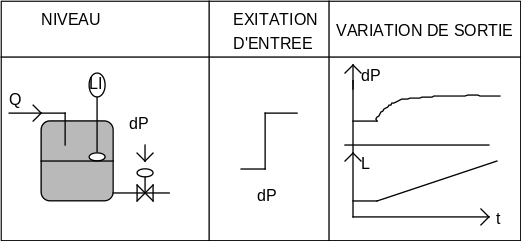
A une excitation d'entrée limitée, correspond une variation de sortie illimitée.
ANALYSE EN BOUCLE OUVERTE
ETUDE DES PROCEDES NATURELLEMENT STABLES
REPONSE DU PREMIER ORDRE SANS TEMPS MORT
Schéma de montage :
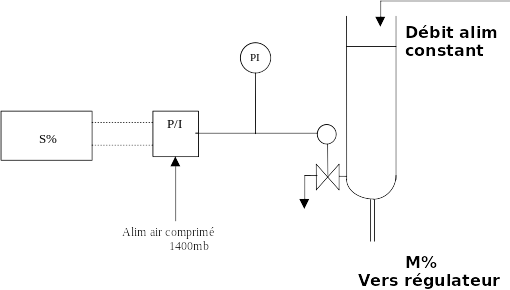
Mode opératoire :
On fixe un débit d’alimentation du réservoir compatible avec le procédé.
Le régulateur étant placé en mode MANUEL, on règle le signal de sortie S% de façon*à stabiliser le niveau (M)dans le réservoir.
Lorsque le niveau est parfaitement stabilisé, on donne une impulsion d’ouverture ou de fermeture de 10 ou 20% en agissant sur le signal de sortie S% du régulateur sans modifier le débit d’alimentation du réservoir.
On note en fonction du temps la variation de la hauteur du liquide dans le réservoir (M%).
Cette valeur peut être lue sur l'échelle graduée ou sur le régulateur.
Etude de la réponse :

On peut déduire de ces courbes :
- Constante de temps θ
- Gain statique Gs =dM/dS
- Temps de réponse Tr : temps mis pour obtenir la stabilisation de la mesure
REPONSE DU PREMIER ORDRE AVEC TEMPS MORT
Etude de la réponse :
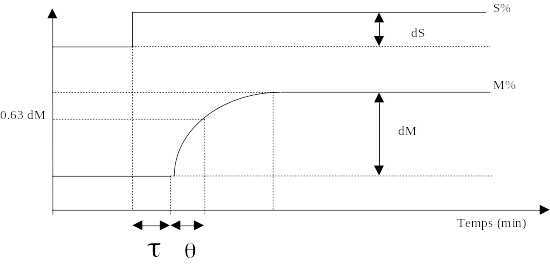
On peut déduire de ces courbes :
Temps mort ι
Constante de temps θ
Gain statique Gs = dM/dS
Temps de réponse Tr
ETUDE DES PROCEDES NATURELLEMENT INSTABLES
SCHEMA :
Le montage est idendique à celui utilisé lors de la précédente étude
MODE OPERATOIRE :
Identique à la précédente étude
ETUDE DE LA REPONSE :

On peut déduire de cette courbe :
Temps mort ι
Constante d’intégration K = (dM/dT)/DS
La connaissance des paramètres déterminés par les méthodes
décrites précédement nous permet de déduire à l’aide des tableaux
suivants l’algorithme de régulation le mieux adapté25
DETERMINATION DE LA LOI DE COMMANDE
PROCEDE NATURELLEMENT STABLE A REPONSE PROPORTIONNELLE
PROCEDE NATURELLEMENT INSTABLE

La loi de commande ayant été définie, On détermine suivant le cas, le GAIN (GR), le TEMPS D’INTEGRALE (TI) et le TEMPS DE DERIVEE (TD) en utilisant les tableaux ci-aprés.
DETERMINATION DES ACTIONS
PROCEDE NATURELLEMENT STABLE A REPONSE PROPORTIONNELLE
Tableau de détermination des actions

PROCEDE NATURELLEMENT INSTABLE

ANALYSE EN BOUCLE FERMEE (Methode de ZIEGLER & NICHOLS)
SCHEMA :
On réalise le branchement de la boucle compléte
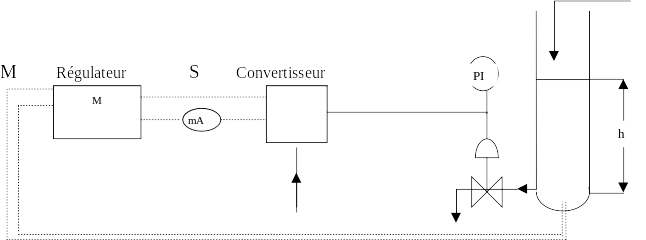
MODE OPERATOIRE :
Le réservoir étant alimenté avec un débit compatible avec le procédé :
Stabiliser la mesure en agissant sur le signal de sortie S%
En utilisant la touche F pour sélectionner le paramètre concerné :
Placer la consigne sur la mesure WL %= M %
Fixer la bande proportionnelle Xp à 100% (G=1)
Temps d’intégrale Ti = 0
Temps de dérivée Td = 0
Vérifier l’absence de signal de sortie (M=C donc S = 0) et la stabilité de la mesure
Donner une impultion de + ou – 10% sur la consigne (C)
Suivre l’évolution de la mesure en fonction du temps
Attendre que celle-ci se stabilise
Augmenter le gain (en diminuant Xp)
Donner une nouvelle impultion sur la consigne
Suivre l’évolution de la mesure en fonction du temps
Renouveller ces manipulations jusqu’à obtenir des oscillations entretenues sur la mesure.
Noter alors la période des oscillations (Tosc)
Noter la valeur de la bande proportionnelle
En déduire le GAIN CRITIQUE DU REGULATEUR (Gcr)
EXEMPLE DE GRAPHES OBTENUS :

TABLEAU DE DETERMINATION DES ACTIONS

LE REGULATEUR
C’est le “Cerveau” de la boucle de régulation.
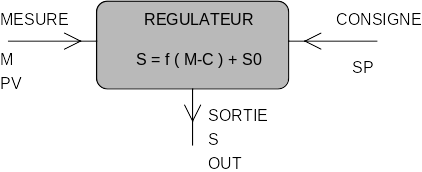
L'équation générale du régulateur s'écrit
\(S = +/-( f( M-C ) + S 0 )\)
dans laquelle :
+/- : le signe dépend du sens d'action du régulateur
+ : sens direct
- : sens inverse
S :signal de sortie (en %)
M : mesure (en %)
C : consigne (en %)
M-C :écart mesure-consigne (en %)
S 0 : décalage (ou bande centrale) (en %)
F étant la fonction de transfert (ou algorithme de régulation)
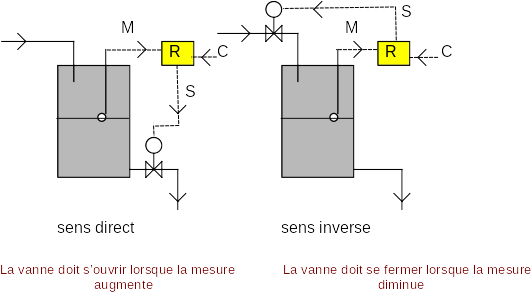
SENS D'ACTION
Selon la configuration du procédé, l'organe correcteur peut être amené à s'ouvrir lorsque l'écart entre la mesure et la consigne devient positif ou, au contraire, à se fermer.
Si le signal de sortie du régulateur varie dans le même sens que l'écart, le sens d'action sera dit DIRECT Si le signal de sortie varie de façon inverse, le sens d'action sera dit INVERSE
EXEMPLE
sens direct
PRINCIPAUX ALGORITHMES DE REGULATION
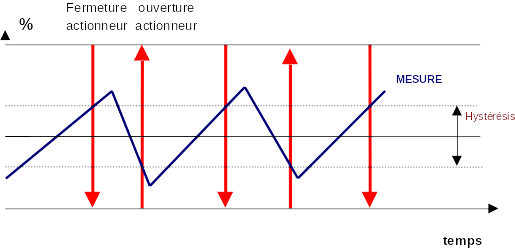
REGULATION TOUT OU RIEN (DISCONTINUE)
Ce mode d'action est essentiellement discontinu. Sa réalisation impose de se fixer une limite inférieure et une limite supérieur.
Lorsque la mesure atteint la limite inférieure, l'actionneur prend une position particulière (arrêt ou marche pour une pompe, ouvert ou fermé pour une vanne).
De façon analogue, le fait d'atteindre la limite supérieure place l'actionneur dans la position contraire. La mesure oscille donc entre ces deux valeurs extrêmes et sa variation prend une l'allure en dents de scie. Ce réglage simple, bon marché présente l'inconvénient d'être peu précis.
D'autre part, ce dispositif ne peut s'appliquer qu'à des installations présentant une inertie suffisamment grande provoquant une fréquence d'oscillation faible afin de ne pas solliciter les organes de commande trop souvent, ce qui réduirait leur durée de vie.

Si X est inférieur à W : Y=0
Si X est supérieur à W : Y =1
ALLURE DES SIGNAUX
ACTION PROPORTIONNELLE (P)
C'est le mode d'action analogique le plus simple. Il convient en général bien aux installations ayant une grande inertie.
SCHEMA DE PRINCIPE :

Le signal de sortie du régulateur est directement (ou inversement, suivant le sens d’action)
proportionnel à l'écart entre la mesure et la consigne
Le coefficient de proportionnalité est noté GAIN (G)du régulateur.
On utilise aussi parfois la notion de BANDE PROPORTIONNELLE (Bp ou Xp) qui est l'inverse ,du gain. Celle ci est exprimée en %.
Bp = 100/G
L’équation de transfert du régulateur s’écrit
\(S \% = +/- G (M-C) +So\)
So, accessible sur certains régulateurs, est appelé décalage ou bande centrale. C’est la valeur du signal de sortie lorsque M=C
ALLURE DES SIGNAUX EN BOUCLE OUVERTE
En boucle ouverte, le signal de sortie du régulateur ne doit pas agir sur
l’actionneur. Pour cela, il suffit que la sortie du régulateur ne soit pas reliée au convertisseur ou que le convertisseur ne soit pas alimenté en air comprimé
A l’instant t=0, on créé un écart mesure – consigne sous forme d’échelon en donnant une impulsion sur la consigne (En général 10%)

L’action proportionnelle seule ne permet pas en général à la mesure de rejoindre la valeur de consigne.
Une augmentation du gain entraîne une réduction de l’écart résiduel mais peut entraîner une instabilité de la mesure. Celle-ci peut devenir oscillante, voire même divergente
ALLURE DES SIGNAUX EN BOUCLE FERMEE

ACTION PROPORTIONNELLE ET INTEGRALE (PI)
L'action intégrale répète l'effet de l'action proportionnelle, jusqu'à ce que l'écart entre la mesure et la consigne soit nul. Elle intègre l’écart M-C en fonction du temps.
La position de l'organe correcteur dépend de l'amplitude et de la durée de l'écart.
L'action intégrale est conditionnée par le temps d'intégrale (Ti) généralement exprimé en minutes.
L’équation de transfert du régulateur devient :
\(S \% = + / − ( G ( M − C ) + G / Ti ( M − C ) dt )\)
ALLURE DES SIGNAUX EN BOUCLE OUVERTE
En boucle ouverte, le signal de sortie du régulateur ne doit pas agir sur l’actionneur. Pour cela, il suffit que la sortie du régulateur ne soit pas reliée au convertisseur ou que le convertisseur ne soit pas alimenté en air comprimé
Exemple :
A l’instant t=0
Ecart mesure – consigne M-C =Constante
G =1
Ti=1 min
Td =0 (pas d’action dérivée)

ACTION PROPORTIONNELLE ET DERIVEE (PD)
\(S \% = + / − ( G ( M − C ) + G . td ( d ( M − C ) / td ) + So\)
L'action dérivée est une action qui tient compte de la vitesse de variation de la mesure (ou de l'écart Mesure-Consigne).
Elle permet d'augmenter la rapidité de la régulation en donnant des impulsions d'ouverture ou de fermeture au signal de sortie. Son usage doit être utilisé avec précaution, ces impulsions ayant tendance à augmenter l'instabilité de la boucle.
Le temps de dérivé (Td) s'exprime en minutes.
L’équation de transfert du régulateur s’écrit :
S % = + / − ( G ( M − C ) + G . td ( d ( M − C ) / td ) + So
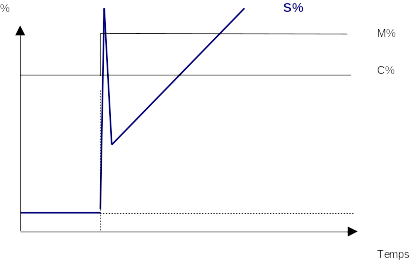
ALLURE DES SIGNAUX EN BOUCLE OUVERTE
Exemple :
A l’instant t=0
Ecart mesure – consigne M-C =Constante
G =1
Td =1
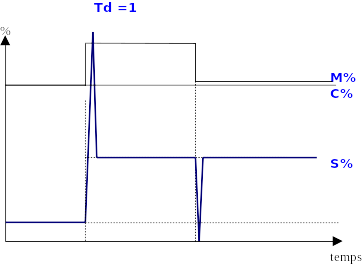
Le signal de sortie fait des pointes nommées «pointes de Dirac »
ACTION PROPORTIONNELLE, INTEGRALE ET DERIVEE (PID)
C'est le type d'algorithme le plus utilisé . Il est en général disponible sur la plupart des régulateurs actuellement utilisés (régulateurs PID).
Il permet la stabilisation de la mesure au point de consigne en un temps minimum.
Equation de transfert :
\(S \% = + / − ( G ( M − C ) + ( G / Ti ) ( M − C ) dt + G . td ( d ( M − C ) / dt )) + So\)
VERIFICATIONS SUR LE REGULATEUR
Toutes ces vérifications s’effectuent en boucle ouverte . La valeur du signal de sortie nedoit pas influer sur la mesure.
Au cours des manipulations, pour créer un écart Mesure / Consigne, il est souvent préférable pour des raisons de commodité, de laisser la mesure stable et de faire varier la consigne.
SCHEMA DE MONTAGE :

CONTROLE DE L’ALIGNEMENT DU REGULATEUR
On fixe la valeur de la consigne à la valeur de la mesure
Le régulateur étant placé en AUTOMATIQUE, en mode proportionnel seul
(ti=0,td=0) le signal de sortie S% doit rester égal à 0 quelles que soient les valeurs du
gain (Xp =100, 10 et 1 par exemple)
CONTROLE DU GAIN DU REGULATEUR
On fixe C = M
Le régulateur étant configuré en mode proportionnel, pour différentes valeurs de Xp (donc de G), on vérifie que le signal de sortie vérifie bien la relation de proportionnalité
S% = G(M-C)
CONTROLE DU TEMPS D’INTEGRALE
On fixe C = M
Le régulateur est configuré en mode proportionnel et intégral
G = 1 (Xp=100)
Ti = 1 min
S% doit être égale à 0
A l’instant To, on donne une impulsion de 10% sur la consigne :
Le signal de sortie doit instantanément prendre la valeur
S% = G(M-C)
La sortie, après ce décalage, doit prendre l’allure d’une rampe
A l’instant To + 1min, la valeur du signal doit avoir doublé
S% = 2 G(M-C)
DETERMINATION DES PERFORMANCES DU REGLAGE
Configurer le régulateur en fonction des paramètres G, ti et td déterminés au cours de l’étude du procédé
Fixer la consigne vers le milieu du réservoir
Se placer un mode MANUEL
Stabiliser la mesure à la valeur de consigne en agissant sur le débit d’alimentation
Se placer un mode AUTOMATIQUE
Provoquer un échelon de + ou – 10% sur la consigne38
Noter l’évolution de la mesure en fonction du temps
Tracer le graphe correspondant
Définir les performances suivantes
STABILITE :
Temps nécessaire pour atteindre une nouvelle valeur stable de la mesure (nouvel équilibre)
PRECISION :
On définit l’erreur de précision Ep
Ep = 100 e/ DetaC

TYPE D’AMORTISSEMENT

PRINCIPAUX TYPES DE BOUCLES DE REGULATION
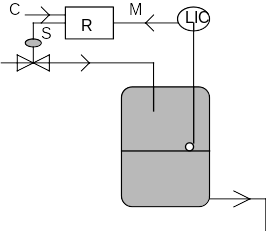
BOUCLE FERMEE
C'est le type de montage le plus utilisé.
Parfaitement fiable, il présente toutefois l'inconvénient d'être lent et de n'assurer qu'une stabilité imparfaite à la mesure.
EXEMPLE
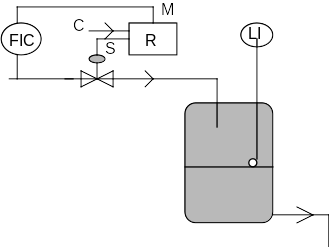
BOUCLE OUVERTE
Ce type de boucle à réponse très rapide n'est pas parfaitement fiable
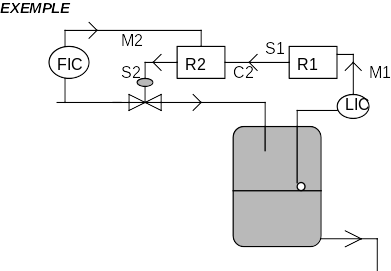
BOUCLE CASCADE
En associant dans ce type de montage une boucle ouverte et une boucle fermée, on obtient à la fois la fiabilité, indispensable à une bonne régulation, et une réponse rapide.
Dans ce montage, la consigne du régulateur est donnée par un autre régulateur appelé : PILOTE. On dit que le régulateur de débit est asservi au régulateur de niveau.
EXEMPLE
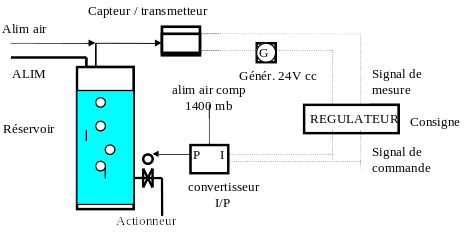
EXEMPLE : BOUCLE DE REGULATION DE DE NIVEAU
Comments