Mechanical Engineering
Pumps Optimum Geometry Versus Specific Speed
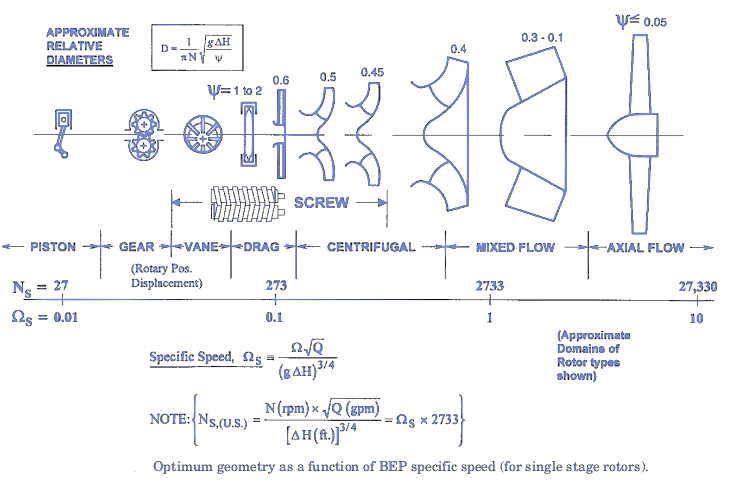
Understanding Pump Optimum Geometry: The Role of Specific Speed
In the world of mechanical engineering, pumps play a crucial role in moving fluids. To design efficient and effective pumps, engineers rely on various parameters, one of which is specific speed (NS or S). This dimensionless group plays a key role in determining the optimum geometry of pump rotors – the heart of the pump's operation.
What is Specific Speed?
Specific speed, a dimensionless parameter, emerges from an analysis of the pump's complete physical equation. This equation relates several factors, including:
- Flow rate (Q): The volume of fluid pumped per unit time.
- Head (H): The total energy added to the fluid by the pump.
- Rotative speed (N): The speed at which the pump rotor spins.
- Rotor diameter (D): The size of the pump rotor.
- Viscosity: The fluid's resistance to flow.
- NPSHA: Net Positive Suction Head Available, indicating the pressure head available at the pump's suction.
Optimum Geometry and Specific Speed
The specific speed (NS) acts as a crucial indicator for determining the optimum geometry of a pump rotor. By analyzing the relationship between specific speed and the head coefficient (cg), we can optimize the pump's efficiency for a given set of operating conditions.
- Lower specific speed: Lower NS values favor rotary positive displacement pumps (vane pumps, gear pumps, screw pumps).
- Higher specific speed: Higher NS values are suited for rotodynamic pumps (impeller pumps), with increasing optimum impeller diameter for higher specific speeds.
Universal Nature of Specific Speed
Specific speed, being dimensionless, remains constant regardless of the units used for its components. This universality makes it a powerful tool for comparing different pump designs and ensuring consistent performance across diverse applications.
Conclusion
Specific speed is a vital parameter for pump design, directly impacting the rotor's geometry and overall efficiency. By understanding its influence, engineers can select the optimal pump type and design for a given application, resulting in efficient fluid handling and minimizing energy consumption.
Test Your Knowledge
Quiz: Understanding Pump Optimum Geometry: The Role of Specific Speed
Instructions: Choose the best answer for each question.
1. What is the specific speed of a pump primarily used for?
a) Determining the size of the pump casing. b) Optimizing the geometry of the pump rotor. c) Calculating the efficiency of the pump motor. d) Measuring the viscosity of the fluid being pumped.
Answer
b) Optimizing the geometry of the pump rotor.
2. Which type of pump is typically associated with lower specific speed values?
a) Centrifugal pumps b) Axial pumps c) Rotary positive displacement pumps d) Turbine pumps
Answer
c) Rotary positive displacement pumps
3. Which of the following factors is NOT directly included in the calculation of specific speed?
a) Flow rate (Q) b) Head (H) c) Rotative speed (N) d) Pump casing material
Answer
d) Pump casing material
4. What makes specific speed a universal parameter?
a) It is always measured in SI units. b) It is a dimensionless quantity. c) It is independent of fluid density. d) It is directly proportional to pump efficiency.
Answer
b) It is a dimensionless quantity.
5. A higher specific speed value typically indicates which of the following?
a) A smaller impeller diameter b) A lower flow rate c) A higher head d) A lower efficiency
Answer
a) A smaller impeller diameter
Exercise: Pump Selection
Scenario: You are tasked with selecting a pump for a water treatment facility. The required flow rate is 1000 m³/h, and the total head is 50 m. You have two options:
- Pump A: Rotary positive displacement pump with a specific speed of 100
- Pump B: Centrifugal pump with a specific speed of 300
Task:
- Analyze the specific speed of each pump and determine which type of pump is better suited for this application. Explain your reasoning.
- Discuss potential advantages and disadvantages of each pump type in this context.
Exercice Correction
**1. Pump Selection:** * Pump A (Rotary positive displacement pump) has a lower specific speed (100), indicating it is better suited for high head, low flow applications. * Pump B (Centrifugal pump) has a higher specific speed (300), suggesting it is more suitable for lower head, higher flow applications. Given the required flow rate (1000 m³/h) and total head (50 m), **Pump B (Centrifugal pump) would be a better choice** for this water treatment facility as it aligns better with the required operating conditions. **2. Advantages and Disadvantages:** **Pump B (Centrifugal pump):** * **Advantages:** * Higher efficiency at the required flow rate. * Lower operating costs. * Generally more compact and require less space. * **Disadvantages:** * Potential for cavitation issues if the suction head is insufficient. * Less robust for handling viscous fluids or fluids with solids. **Pump A (Rotary positive displacement pump):** * **Advantages:** * More robust for handling viscous fluids or fluids with solids. * Constant flow rate regardless of pressure changes. * **Disadvantages:** * Lower efficiency at the required flow rate. * Higher operating costs. * Typically larger and require more space. **Conclusion:** In this scenario, the higher specific speed centrifugal pump (Pump B) appears to be the more appropriate choice due to its greater efficiency and suitability for the required flow rate and head. However, if the application involved handling viscous fluids or fluids with solids, the rotary positive displacement pump (Pump A) might be a better option despite its lower efficiency.
Books
- "Pump Handbook" by Igor J. Karassik, William C. Krutzsch, Joseph P. Fraser, and Joseph Messina: This comprehensive book delves into various aspects of pump design, including specific speed and its impact on pump geometry.
- "Centrifugal Pumps: Design and Application" by A.J. Stepanoff: This classic textbook offers detailed explanations of centrifugal pumps, covering topics like specific speed, impeller design, and pump performance.
- "Fluid Mechanics" by Frank M. White: This textbook provides a solid foundation in fluid mechanics, essential for understanding the principles behind pump operation and specific speed.
Articles
- "Specific Speed and Pump Design" by The Hydraulic Institute: This article provides a practical overview of specific speed and its role in selecting appropriate pumps for various applications.
- "Optimizing Pump Performance by Understanding Specific Speed" by Pumps & Systems Magazine: This article explores the relationship between specific speed and pump efficiency, highlighting its importance in design and selection.
- "The Importance of Specific Speed in Pump Selection" by Fluid Handling Magazine: This article discusses the significance of specific speed in ensuring optimal pump performance and minimizing operating costs.
Online Resources
- Hydraulic Institute: This organization offers comprehensive resources on pumps and pumping systems, including articles, standards, and educational materials. https://www.hydraulicinstitute.org/
- Pump Industry Association: This association provides information on pumps and pumping systems, including technical resources and industry news. https://www.pumps.org/
- Pumping Machinery Research Association (PMRA): This organization focuses on research and development related to pumping systems, offering valuable insights into pump design and performance. https://www.pmra.org/
Search Tips
- "specific speed pump design"
- "optimum geometry pump impeller"
- "pump performance specific speed"
- "centrifugal pump selection specific speed"
- "pump efficiency specific speed"
- "hydraulic institute specific speed"
Techniques
Chapter 1: Techniques for Determining Optimum Geometry
This chapter delves into the techniques used to determine the optimum geometry of a pump rotor based on its specific speed (Ns).
1.1. Dimensional Analysis and Scaling Laws:
- Buckingham Pi Theorem: This theorem is used to derive dimensionless groups like specific speed (Ns), head coefficient (cg), and flow coefficient (cq). These dimensionless groups allow for scaling of pump designs and comparing pumps of different sizes.
- Affinity Laws: These laws relate the performance parameters of a pump (head, flow rate, power, and efficiency) to changes in speed, impeller diameter, and fluid properties.
- Model Testing: Using scaled-down models of pumps, experimental data is gathered to validate theoretical predictions and optimize design parameters.
1.2. Computational Fluid Dynamics (CFD):
- Numerical Simulation: CFD software simulates fluid flow through the pump impeller, providing detailed information on velocity, pressure, and energy distribution.
- Optimization Algorithms: These algorithms utilize CFD simulations to search for the best impeller geometry that maximizes efficiency and minimizes energy loss.
- Validation: CFD simulations are validated against experimental data or established performance curves to ensure accuracy.
1.3. Experimental Techniques:
- Performance Testing: Testing a pump in a dedicated test facility to measure its head, flow rate, power consumption, and efficiency at various operating points.
- Cavitation Tests: Evaluating the pump's susceptibility to cavitation, a phenomenon that can damage the pump and reduce efficiency.
- Noise and Vibration Analysis: Determining the noise and vibration levels generated by the pump, important for minimizing noise pollution and ensuring reliable operation.
1.4. Analytical Methods:
- Empirical Formulas: These formulas, based on past experience and data analysis, predict pump performance based on specific speed and other design parameters.
- Theoretical Models: Simplified mathematical models can be used to analyze the flow through the impeller and predict the pump's performance.
1.5. Design Considerations:
- Impeller Design: Factors like blade shape, number of blades, and hub ratio influence the flow pattern and pump efficiency.
- Volute Design: The volute surrounding the impeller collects the flow and directs it to the discharge pipe.
- Shaft Design: The shaft transmits power to the impeller and must be strong enough to withstand the operating loads.
Conclusion:
By employing these techniques, engineers can determine the optimum geometry of a pump impeller, resulting in a more efficient, reliable, and cost-effective pumping solution.
Chapter 2: Pump Models and Specific Speed
This chapter explores the relationship between specific speed (Ns) and the different types of pumps, highlighting the optimum geometry for each model.
2.1. Rotary Positive Displacement Pumps:
- Low Specific Speed (Ns < 50): These pumps, such as vane pumps, gear pumps, and screw pumps, typically operate at low flow rates and high pressures.
- Optimum Geometry: Compact design with tight clearances between the rotating elements and the casing.
- Characteristics: Constant flow rate regardless of pressure changes, high torque, and pulsating flow.
2.2. Rotodynamic Pumps:
- Centrifugal Pumps:
- Moderate Specific Speed (Ns = 50 - 150): Widely used in various applications due to their versatility and relatively high efficiency.
- Optimum Geometry: Impeller with curved blades, usually with a single stage.
- Characteristics: High flow rates at moderate heads.
- Axial Flow Pumps:
- High Specific Speed (Ns > 150): Suitable for high flow rates and low heads.
- Optimum Geometry: Impeller with axial blades, often with multiple stages.
- Characteristics: Low head rise, high flow rate, and compact design.
- Mixed Flow Pumps:
- Intermediate Specific Speed (Ns = 50 - 150): Combines features of both centrifugal and axial flow pumps.
- Optimum Geometry: Impeller with blades angled between radial and axial, often with multiple stages.
- Characteristics: High flow rates and moderate heads.
2.3. Pump Selection Based on Specific Speed:
- Selecting the Right Pump: Understanding the specific speed of a pump application is crucial for choosing the most efficient and cost-effective pump type.
- Matching Specific Speed and Application: Pumps with specific speeds that align with the required flow rate, head, and operating conditions will achieve optimal performance.
Conclusion:
Specific speed serves as a valuable tool for selecting the appropriate pump model and optimizing its geometry. Matching the specific speed to the application ensures efficient operation and optimal performance.
Chapter 3: Software for Pump Design and Analysis
This chapter discusses the various software tools available for pump design and analysis, highlighting their capabilities in relation to specific speed and pump geometry.
3.1. CFD Software:
- Ansys Fluent, Star-CCM+: These widely used CFD software packages allow engineers to simulate the flow through pump impellers, providing insights into velocity, pressure, and energy distribution.
- OpenFOAM: An open-source CFD software, gaining popularity for its flexibility and customizability.
- Features:
- Mesh Generation: Creating a computational mesh of the pump geometry for accurate fluid flow simulation.
- Solver Capabilities: Solving the Navier-Stokes equations to model the fluid flow and predict performance.
- Post-processing: Analyzing and visualizing the simulation results, including velocity profiles, pressure contours, and efficiency maps.
3.2. Pump Design Software:
- PumpLinx, PumpFLO: These specialized software programs focus on pump design, optimization, and performance analysis, incorporating specific speed considerations.
- Features:
- Impeller Design Tools: Creating and modifying impeller geometry based on specific speed and operating conditions.
- Performance Prediction: Generating performance curves and efficiency maps for different pump configurations.
- Cavitation Analysis: Predicting the onset of cavitation and its impact on pump performance.
3.3. Data Analysis and Visualization Tools:
- MATLAB, Python: These programming languages provide robust tools for data analysis, visualization, and automation of design tasks.
- Excel, Tableau: Spreadsheets and data visualization tools can be used for analyzing experimental data, creating performance curves, and generating reports.
3.4. Cloud-based Platforms:
- AWS, Azure, Google Cloud: Cloud-based platforms offer scalable computing resources for running complex CFD simulations and collaborating on pump designs.
Conclusion:
Advances in software tools are enabling engineers to design and analyze pumps with increased accuracy and efficiency. These tools leverage specific speed to optimize pump geometry and achieve desired performance targets.
Chapter 4: Best Practices for Pump Design and Optimization
This chapter outlines the best practices for pump design and optimization, focusing on the importance of specific speed and its impact on overall performance.
4.1. Understand the Application Requirements:
- Flow Rate and Head: Precisely determine the required flow rate and head for the application to select the appropriate pump type and specific speed.
- Fluid Properties: Consider the viscosity, density, and other characteristics of the fluid to be pumped.
- Operating Conditions: Evaluate the operating pressure, temperature, and potential for cavitation to optimize pump design.
4.2. Optimize Impeller Geometry:
- Blade Shape and Angle: Design the impeller with the appropriate blade shape and angle to maximize efficiency and minimize energy loss.
- Number of Blades: Consider the number of blades based on the specific speed and flow rate requirements.
- Hub Ratio: Optimize the hub ratio (ratio of hub diameter to impeller diameter) for efficient flow and performance.
4.3. Minimize Losses:
- Hydraulic Losses: Reduce friction losses in the flow path by optimizing the impeller design, volute shape, and flow passages.
- Mechanical Losses: Minimize losses in the bearings, seals, and shaft by using appropriate materials and lubrication.
- Cavitation Control: Design the pump system to prevent cavitation by ensuring adequate NPSHA.
4.4. Consider Efficiency and Life Cycle Costs:
- Pump Efficiency: Strive for high pump efficiency by optimizing the impeller design and minimizing losses.
- Life Cycle Costs: Evaluate the long-term costs of the pump, including energy consumption, maintenance, and replacement, to select a cost-effective solution.
4.5. Implement Verification and Testing:
- CFD Simulation: Use CFD simulations to validate the design and predict performance before physical prototyping.
- Performance Testing: Conduct comprehensive performance testing of the pump to verify its efficiency and ensure it meets the application requirements.
Conclusion:
By adhering to these best practices, engineers can design and optimize pumps with high efficiency, reliable operation, and long-term performance.
Chapter 5: Case Studies
This chapter presents real-world case studies highlighting the practical application of specific speed in optimizing pump geometry and achieving improved performance.
5.1. Case Study 1: Water Supply System Optimization:
- Challenge: A municipality's water supply system faced low efficiency and high energy consumption.
- Solution: By analyzing the specific speed requirements and optimizing the pump design, engineers replaced inefficient pumps with high-efficiency models, resulting in significant energy savings and improved system performance.
5.2. Case Study 2: Industrial Process Pump Upgrade:
- Challenge: An industrial process pump experienced cavitation issues, leading to reduced performance and premature wear.
- Solution: Using CFD simulations and specific speed considerations, engineers redesigned the impeller and optimized the NPSHA, eliminating cavitation and improving pump efficiency.
5.3. Case Study 3: Wastewater Treatment Plant Improvement:
- Challenge: A wastewater treatment plant required a pump capable of handling high flow rates and abrasive fluids.
- Solution: By considering the specific speed and the aggressive nature of the fluid, engineers selected a pump with a robust design and appropriate materials, ensuring long-term reliability and efficiency.
Conclusion:
These case studies demonstrate the practical application of specific speed in solving real-world pump design challenges. By leveraging specific speed and employing best practices, engineers can optimize pump performance, improve efficiency, and minimize energy consumption.
- ASME Specifications ASME Specifications: Guiding …
- rotary speed Rotary Speed: A Key Factor in…
- Classification Of Pumps Deciphering the World of Pump…
- Pumps Selection Pump Selection in Mechani…
- Design-to Specifications Designing for Success: Unders…
- Gravity Specific Understanding Specific Gravit…
- Interface Requirements Specification Interface Requirements Specif…
- Interface Specification Interface Specification: A Cr…
- Software Product Specification Software Product Specificatio…
- Monitoring Actuals versus Budget Keeping the Oil Flowing: Moni…
- Performance Specification Performance Specification: Th…
- Ratio of Specific Heats The Ratio of Specific Heats: …
- Rotary Speed Rotary Speed: Understanding t…
- Specific "Specific" in Oil & Gas: Beyo…
- Specification Unveiling the Blueprint: Spec…
- Specification Specifications: The Blueprint…
- Report Specification File The Unsung Hero of Data: Unde…
- Requirement Specification Requirement Specification: Th…
- Software Specification Review Software Specification Review…
- Specification The Power of Specifications i…
- Application for Expenditure Justification Navigating the Appl… Project Planning & Scheduling
- Budgeted Cost of Work Scheduled ("BCWS") Understanding Budge… Cost Estimation & Control
- Battery limit Understanding Batte… General Technical Terms
- DV Tool (cementing) DV Tool: A Crucial … Drilling & Well Completion
- TOC TOC: Understanding … General Technical Terms
Comments