Estimation des coûts d'équipement | Partie 2
cost-estimation equipment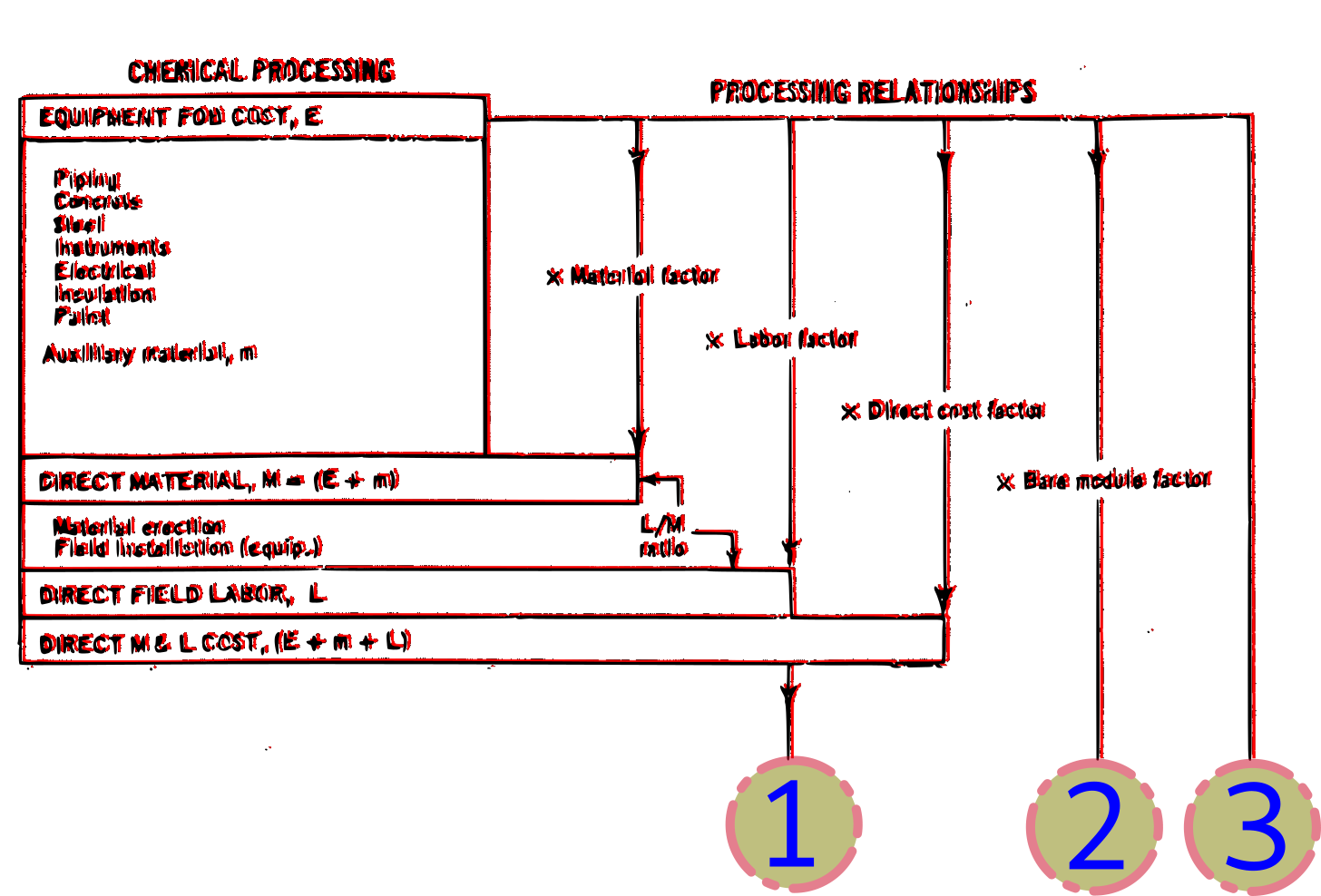
PARTI 1 PARTI 2
Sommaire de la partie 1
Aperçu
Objectif
Public visé
Avantages pour les lecteurs
Contenu
Types d'estimation des coûts et précision
Estimation des coûts d'équipement de processus par ratio et indice
La règle des six dixièmes
Indices de coût
Partie 2
Exemple
L'exemple suivant illustre une utilisation combinée de ces deux méthodes de ratio et de d'indice de prix pour produire un coût approximatif.
Veuillez noter que les coûts présentés ici sont illustratifs.
Supposons que nous avons à estimer approximativement, pour une affaire en cours de préparation pour un projet dans lequel il y a un appreil sous presssion d'une capacité de 60 m³ en acier inoxydable.
Supposons en outre que dans l'historiques des achats de projets réalisés antérieurs nous trouvons un récipient sous pression en acier inoxydable de 20 m³, très similaire à celui actuellement requis, et qui a été acheté en 2012 pour 15 000 $.
Nous avons maintenant tous les céléments nécessaires pour estimer le coût actuel (C B ) de notre appreil de 600m³.
Nous avons, deux dates, celle de la commande de précedent appareil et bien sûr l'actuelle :
deux capacités connues (\(S_A\)et \(S_B\) )
un coût historique (\(C_o\) ) (celui de 2012 )
La première étape consiste à déterminer l'indice de coût pour nos deux dates.
En consultant l'indice du cout de l'acier inoxydable en 2013 l'indice nous trouvons qu'il etait à 5.006 (notre indice de base pour cet exemple).
De la même manière, l'indice du 1er trimestre 2023 s'avère être 13,53 (l'indice actuel).
Cette différence du coôut est en fait l'inflation, du prix de l'acier inoxydable qui a eu lieu entre ces deux dates .
Estimation des coûts d'équipement de processus par ratio et indice
Ces données compilées nous permettent de calculer
\(C = C_0 \bigg( {I\over I_0} \bigg) = (15 000) \bigg( {18.450\over 5.620} \bigg) = 49243.772\)
Par conséquent, le coût de l'appreil d'une capacité de 20 m³ aurat couté au 1er trimestre 2023 49243.772 $.
Maintenant, après avoir déterminé le coût estimatif actuel de l'appareil de plus petite capacité, nous devons ajuster ce montant correspond au plus grand volume de 60 m³. En se référant au tableau exposé en partie 1, nous trouvons un exposant de taille correspondant aux récipients en acier inoxydable égal à 0,68.
Calculons l'équation avec les précédents résultats cela donne cce qui suit :
\(C_B = C_A \bigg( {S_B\over S_A}\bigg)^N = 48000 \bigg({60\over 20}\bigg)^{0.68 }= 103904.358\)$
nous majorons donc le coût à [104 000 $] qui sera notre estimation à plus ou moins 15 %.
Par conséquent, le coût approximatif d'un appareil d'une capacité de 60 m³ au 1er trimestre 2023 est 140 000 $.
Comme le projet ne sera réalisé que dans 2 trimestre, nous que selon la courbe de tendance de notre indice serait à 22.25, nous réjutons notre estimation en conséquence.
\(C_f = C \bigg( {I_t\over I} \bigg) = (104000) \bigg( {22.25\over 18.450} \bigg) = 125.420\)
Donc nous allons figer notre estimation \(C_f\) à 125 K$
Bien entedu nous pouvons faire nos calculs avec une calcualtrice scientifique ou avec un tableur mais le mieux et le plus efficace pour en garder un historique c'est de le faire avec des script sauvegardant les input et les output à travers une page html ou simplement sur votre console.
Voici un exemple de calcul des six dixièmes
#This program will calculate the six tenths factor of any given number
#Function definition to calculate the six tenths factor
def sixTenthsFactorCalculation(n):
return ((n + (6/10) + (n*(6/10))) / 2 )
#Main Program
#Input will be taken from user and verified whether it is a number or not
userInput = input("Enter the number to calculate six tenths factor: ")
if userInput.isnumeric():
number = int(userInput)
#Calculate the six tenths factor
result = sixTenthsFactorCalculation(number)
print("The six tenths factor of {} is {}".format(number, result))
else:
print("Please enter a valid number")
Voila un exemple de calcul du cout de tendance en python.
/declare Variables
var prices = [1, 8, 6, 19, 21, 12];
var sum = 0;
var average;
var trend;
//get sum of all prices
for (var i = 0; i < prices.length; i++) {
sum += prices[i];
}
//calculate average
average = sum / prices.length;
//determine trend
if (prices[prices.length-1] > average) {
trend = 'Prices are increasing.';
} else if (prices[prices.length-1] < average) {
trend = 'Prices are decreasing.';
} else {
trend = 'Prices are not changing.';
}
//print trend
console.log(trend);
Comments